2024년 9월 고1 수학 모의고사 객관식 (19~21번)

지난 시간에 이어 객관식 마지막 3문항 마저 풀이해 보겠습니다. 잘 따라오고 계시죠?^^

19번

• 최고차항 계수의 절댓값이 같다라는 조건과, (가) 조건에서 두 이차함수를 뺐더니 최고차항의 계수가 -4인 이차식이 도출되었습니다. 따라서 f의 최고차항 계수는 -2, g의 최고차항 계수는 2라는 것을 알 수 있습니다.
• 추가로, 두 이차함수의 교점의 x좌표가 -3, 2라는 정보도 바로 캐치할 수 있어야 합니다. 교점의 좌표라는 것은 두 함수를 연립하였을 때 해를 말하는데, (가) 조건에서 바로 알 수 있죠?
• 교점을 A, B라고 하였을 때 직선AB의 기울기는 -1 : 직선 AB를 빗변으로 하는 직각삼각형이 가로길이와 세로길이가 같은 직각이등변삼각형이 될 수 있다는 것 유추가능합니다. 
• 그림을 그려 설명하겠습니다. 

19번풀이

20번

• 직선PC가 삼각형 AOB의 넓이를 이등분한다 : 삼각형 AOB의 넓이를 S라고 한다면, 직선 PC를 기준으로 각각 (1/2)S가 됩니다. 추가로, 꼭짓점 O에서 직선 AB의 2:1 내분점인 P까지 보조선을 그리고, 직선 PC와 선분 AO의 교점을 Q라고 한다면, 삼각형 PQO는 (1/6)S가 됩니다. 그림을 그려 설명하겠습니다.

20번풀이

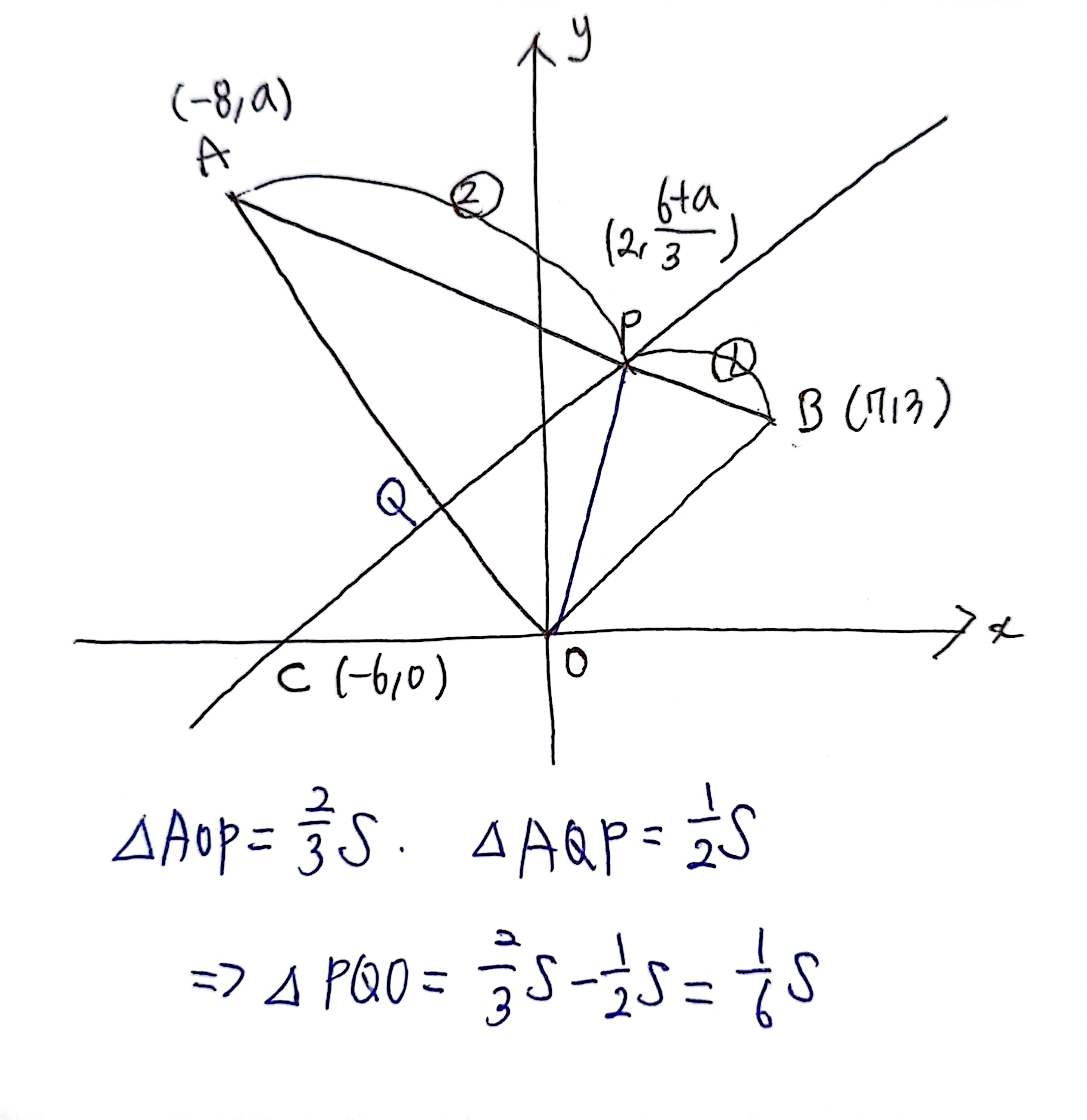
• 선분 PC는 삼각형을 절반으로 잘랐습니다.
• 점 P는 선분 AB를 2:1로 내분한 점입니다. 그 점과 삼각형의 꼭짓점을 연결하면 삼각형의 넓이도 2:1로 나뉩니다. 따라서 위와 같이 삼각형 PQO를 (1/6)S로 나타낼 수 있습니다.
• 내분점 P의 좌표는 내분점 공식을 이용하여 구하였습니다. 
• 다음은 Q의 좌표를 구해야 합니다. 삼각형을 2:1로 내분하는 관점으로 본다면, 점 Q는 이번에는 선분 AO를 3:1로 내분하는 점입니다. 왜냐하면 삼각형 AQP는 (1/2)S, 삼각형 PQO는 (1/6)S이기 때문에 1/2:1/6 = 3:1입니다.
• 내분점 구하는 공식 적용하면 Q의 좌표는 Q(-2, a/4)가 됩니다. 
• 이제 양수 a를 구하기 위하여 선분 PQ와 직선 PC의 기울기가 같다는 점을 활용합니다.
• 기울기 = (y증가량)/(x증가량)
• PQ의 기울기 = [(6+a)/3 - a/4] / 4
• PC의 기울기 = [(6+a)/3] / 8
• 두 기울기가 같다고 식을 두고 풀면 a의 값은 12가 나옵니다. 

 

21번

• a, b, c가 양수라는 점, f와 g가 아래로 볼록, 위로 볼록이라는 점 외에는 그래프에 대한 정보는 없습니다.
• 다만 조건에서, y=k라는 가로선이 서로 다른 세 점에서만 만나는 선은 오로지 2와 3뿐이다라고 하였습니다.
• g를 고정시키고, f를 왼쪽에서 조금씩 오른쪽으로 옮겨가며 맞는 조건을 찾아보겠습니다.

21번풀이

 

 

21번풀이

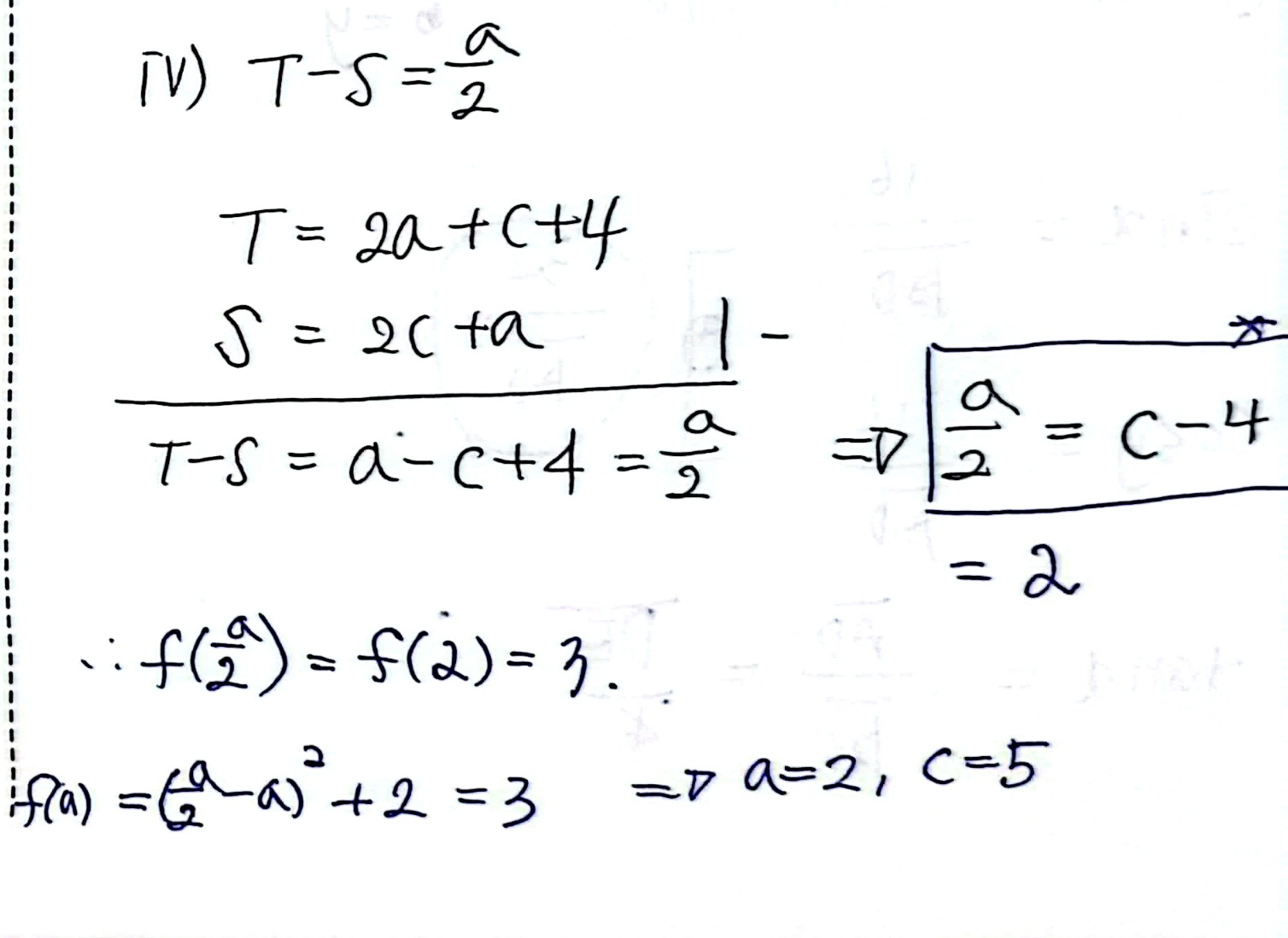
따라서 21번의 답은 5번입니다. 

다음은 단답형의 4점짜리 문항으로 찾아뵙도록 하겠습니다. 모두 파이팅!^^

2024년 9월 고1 수학 모의고사 객관식 (14~18번)

2025학년도 9월 고1 수학 모의고사 객관식 (14~18번)